立ち読み・第１章より ②

人間の非合理さを露呈させる簡単な確率の問題

　１９５０年代から１９８０年代にかけて、テレビのゲーム番組が人気を博したが、そのなかでもとりわけ人気が高かった番組の一つに『レッツ・メイク・ア・ディール』というのがある。司会者のモンティ・ホールはこの番組で有名になっただけではなく、番組がきっかけで知られるようになった確率論のジレンマが「モンティ・ホール問題」と命名されたことによって、二重の意味で有名になった。

　この番組のゲームは次のようなものだ。参加者の前に３つのドアが用意されていて、１つのうしろにはピカピカの新車が、残り２つのうしろにはヤギが隠されている。参加者はどれか１つのドア（ドア１としよう）を選ぶ。それからモンティが、場を盛り上げるべく、残り２つのドアの片方（ドア３としよう）を開くと、そこにはヤギがいる。さらに場を盛り上げるべく、モンティは参加者にドア１のままでいいか、それとももう１つのドア（ドア２）に変えるかと訊く。さあ、あなただったらどうする？

　ほとんどの人は選択を変えない。車が隠されているのは３つのドアのうちのどれかだが、ドア３は違うとわかったので、今やドア１かドア２の２択で、勝率はどちらも50パーセントだと考える。つまり選択を変えても損はないが、結局のところ変えても変えなくても同じだと考える。そういう場合、人は惰性やプライドから、あるいは変えて当たったときの喜びより変えてだめだったときのショックのほうが大きいだろうと思い、変えないほうを選ぶ。

　モンティ・ホール問題が有名になったのは、１９９０年に『パレード』誌の「マリリンに訊いてみよう（Ask Marilyn）」というコラムで紹介されたからで、この雑誌はアメリカの何百もの新聞の日曜版に折り込まれていたので多くの人の目に留まった。マリリンというのはコラムニストのマリリン・ヴォス・サヴァントのことで、ＩＱのギネス記録をもっているため“世界一賢い女性”として知られていた。

　そのヴォス・サヴァントがこのゲームについて問われ、「車がドア２のうしろにある確率は３分の２、ドア１のうしろにある確率は３分の１だから、選択を変えたほうがいい」と答えた。するとこのコラムに１万通もの手紙が寄せられ、そのうち１０００通は主に数学や統計学の博士たちからのもので、そのほとんどがマリリンの間違いを指摘していた。 　

　著名な数学者ポール・エルデシュ（１９１３─１９９６）でさえ、当初は反論する側だった。彼は実に多くの論文を書き、共著者も多かったので、エルデシュとの関係の近さを示す「エルデシュ数」〔数が小さいほどエルデシュに近い。エルデシュと直接の共著論文がある人は１、１の人と共著論文があれば２、２の人と共著論文があれば３……と関係が遠ざかるほど数が増えていく〕というのが学者たちの自慢の種になっているほどなのだが、そのエルデシュもマリリンの説に納得がいかなかった。

　しかしながら、間違っていたのは反論した学者たちのほうで、“世界一賢い女性”は正しかった。あなたが参加者なら、選択を変えたほうがいい。

　その理由もそれほどややこしくはない。車がどこに置かれているかには、ドア１、ドア２、ドア３の３通りの可能性がある。この３通りそれぞれを考えて、選択を変えない場合と変えた場合の“当たり”の回数を数えてみよう。あなたはドア１を選んだ。これは単なるレッテルなので何番のドアでもいい。モンティが「選ばれていないドアのうちヤギがいるドアを開ける。両方にヤギがいるならその片方をランダムに選ぶ」というルールを守っているかぎり、最初にどのドアを選んでも確率は変わらない。

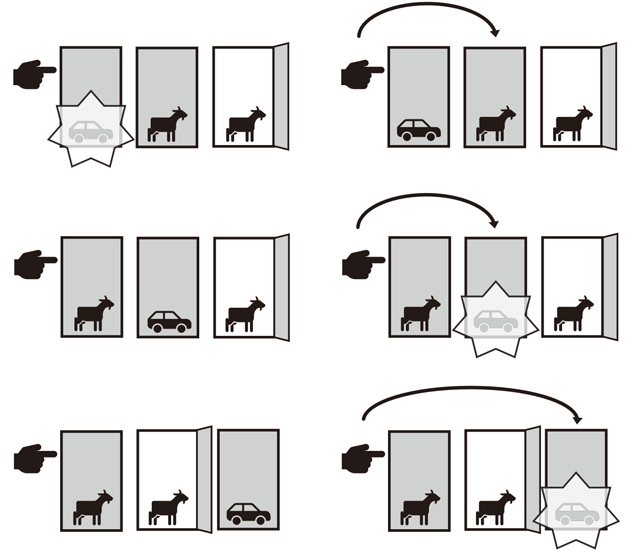
　まずあなたが「選択を変えない」場合を考えてみよう（図の左側の列）。図のドアを左から１、２、３とする。車がドア１にあれば、あなたの勝ち（あなたは選択を変えないのだから、モンティがドア２と３のどちらを開けるかは関係ない）。車がドア２にあれば、あなたの負け。車がドア３にあれば、あなたの負け。つまり「選択を変えない」場合の勝率は３分の１である。

　次にあなたが「選択を変える」場合を考えよう（図の右側の列）。車がドア１にあれば、あなたの負け。車がドア２にあれば、モンティがドア３を開けるはずなので、あなたはドア２に切り替え、あなたの勝ち。車がドア３にあれば、モンティがドア２を開けるはずなので、あなたはドア３に切り替え、あなたの勝ち。つまり「選択を変える」場合のあなたの勝率は３分の２で、「選択を変えない」場合の２倍になる。

　難解というほどのものではない。論理的な可能性など考えずに、切り絵やおもちゃを使って何度かやってみて、勝ち負けを数えてみるだけでわかる。実際モンティ・ホールはそうやってある懐疑的なジャーナリストを説得した（今ならインターネット上でシミュレーションすることもできる）。

　あるいは、「モンティは答えを知っていてヒントをくれたわけだから、それに応じないのはばかげている」という直感から考えてみてもいい〔モンティが車の置かれたドアを開けることは決してないというところがポイント〕。それなのに、なぜ多くの数学者、大学教授、その他の大物は間違えてしまったのだろうか。

　「立ち読み①」で紹介したウェイソン選択課題に潜んでいた問題と同じように、モンティ・ホール問題にもわたしたちの「直感的な思考回路」に間違いを犯させるような要素が含まれている。しかも今回は「熟慮を司る思考回路」もうまく機能しない。多くの人が、正しい答えの説明を聞いてもなお納得できないのはそのためだ。エルデシュもその一人で、数学者のプライドをかなぐり捨ててこのゲームのシミュレーションを何度も見て、ようやく納得したそうだ。

　だがシミュレーションを見ても、実際に自分でやってみても、どうしても納得できないという人が少なくない。ではこのゲームの確率の法則と、わたしたちの直感は、どこがずれているのだろうか？

　ヒントの一つは、マリリンに反論した自信過剰の人々が、自分の考えをどう正当化したかに隠されている。そこには、時に軽率に、他の確率パズルの考え方が持ち込まれていた。

　たとえば多くの人は、未知の選択肢（ここではまだ開けられていないドア）の確率は皆等しいと思い込む。それはコインの裏表やサイコロの目のような、対称になっているギャンブルの小道具には当てはまるし、同じ選択肢でもあなたが何も知らない状態で最初の１つを選ぶときには当てはまる。だがそれは自然法則ではない。

　多くの人は、因果連鎖を頭のなかで描き出す。１台の車と２頭のヤギは最初からドアの向こうに配置されていて、ドアが１つ開いたからといって、そのあとであちこち動いたりはできない。このような因果メカニズムの独立性を指摘することは、ほかの場合においては錯覚に気づかせるための一般的な方法で、「ギャンブラーの誤謬」についてもそうだ。ギャンブラーの誤謬に陥った人は、ルーレットで赤が続くと次は黒の確率が上がると思い込む。だがルーレットに記憶などあるはずもなく、一回一回はあくまでも独立した事象である。

　ヴォス・サヴァントに手紙を送ってきた学者の一人はこう書いていた。「それぞれの勝率が等しい３頭の馬のレースを思い浮かべてください。スタートから50フィートのところで馬３が倒れたとしたら、残った馬１と馬２の勝率はそれぞれ３分の１ではなく、２分の１になるわけです」。したがって、馬１から馬２に乗り換えても何の意味もないことは明らかだと彼は結んでいる。

　ところがモンティ・ホール問題はそれとは仕組みが異なる。あなたが馬１に賭けたあとで、天から神の声が聞こえてきて、「勝つのは馬３ではないぞ」と告げたと想像してみてほしい。「馬２」について警告を発することもできたかもしれないのに「馬３」と告げたのだ。だとしたら馬１から馬２に乗り換えるのはそれほどおかしなことではない。『レッツ・メイク・ア・ディール』ではモンティ・ホールがその神だった。

　司会者のこの“神の立場”に目を留めれば、モンティ・ホール問題の風変わりな点に気づくことができる。つまりこの問題では、司会者は会話の通常の目的──聞き手が知るべき情報（この場合なら、どのドアに車が隠されているか）を共有すること──を無視し、視聴者の緊張感を高めることを目的としている。そのためには、司会者は“全知の存在”である必要があるのだ。普通の世界でわたしたちがヒントを探すとき、そのヒントはわたしたちの探索とは無関係に存在するが、全知のモンティは答えを知っていて、わたしたちの選択も知っていて、それに応じてヒントを出してくる。

　この謎めいた、だが有用なヒントに人々が鈍感だという事実こそが、この問題の核心にある認知の弱点を教えてくれる。すなわち、確率を傾向と混同するという弱点のことである。傾向とは、ある対象の状態や動きが何らかの偏りを見せることをいう。傾向についての直感は、世界に関するわたしたちのメンタルモデル〔行動の結果を予測したり、結論を導いたりするときに利用される、経験や知識を基にした前提〕の大きな部分を占めている。

　たとえば人は、「曲げられた枝は跳ね返りやすい」とか、「ヤマアラシは肉球跡が２つの足跡を残しやすい」といった感覚をもちうる。傾向は直接感知することはできない（枝が跳ね返ったところか、跳ね返らなかったところしか見ることができない）が、対象の物理的構造をよく調べ、それを因果律と突き合わせることによって推測できる。乾燥した枝は跳ね返らずに折れるかもしれない、というのも傾向である。

　だが確率はこれとは異なり、17世紀に発明された概念ツールである。「確率」には複数の解釈があるが、リスクを伴う判断にとって重要なのは「未知の事象に対するあなたの確信の度合い」だろう。だからある結果へのわたしたちの確信を変えるような証拠が一つでも出てきたら、その結果の確率は変わるし、それに基づいた合理的な行動も変わる。確率は物理的傾向性だけではなく、物理的実体のない「知識」にも依存しているということが、人々がモンティ・ホール問題でつまずく理由となっている。彼らはこういう場合、車はすでにドアの１つのうしろに置かれていて動かせないという傾向を感覚としてつかんでいて、司会者がドアの１つを開けてもその傾向を変えられたはずはないと知っている。しかし確率は世界に関係するのではなく、世界についてのわたしたちの“無知”に関係する。新しい情報はわたしたちの無知を減らし、確率を変える。

　まだぴんと来ない、どこか変だと思う人は、わたしがたった今投げたコインが表向きになっている確率について考えてみてほしい。表の確率はあなたにとっては50パーセントだが、わたしにとっては１００パーセントだ（ちらりと見たから）。同じ出来事でも知識が変われば確率も変わる。モンティ・ホール問題では、すべてを見ている司会者が新情報を提示するのだから、当然確率も変わる。

　そこで一ついえるのは、司会者の助けによる無知の減少が、もっとあからさまな物理的状況に結びつけば、この問題の答えも直感的にわかるようになるということだ。実際ヴォス・サヴァントは、もっとたくさん（たとえば１０００枚）ドアがある場合を想像してみてくださいと読者に呼びかけた。あなたはそのなかの１つを選ぶ。続いてモンティが９９８枚のドアを開ける（すべてヤギが現れる）。残ったドアはあなたが選んだドアとモンティが残したドアの２つだけ。さあ、どうする？

　ここまで数が増えれば、モンティの選択は意志決定に使える情報だと思えるだろう。わたしたちは彼がどのドアを開けるか決めるために、車がどこにあるかを確認している様子を思い浮かべることができるし、そうなれば、彼が開けなかったドアは彼がそのうしろに車を見つけたというヒントであり、したがって車そのもののヒントだと思えるはずだ。