立ち読み・第1章より ③
人間の非合理さを露呈させる簡単な予測の問題
予測事業は今や一大ビジネスに成長している。予測は政策、投資、リスク管理、あるいは純粋な好奇心のために、この先、何が待ち構えているかを教えてくれるのだから当然のことだろう。
ではここで、次に挙げる8つの事象について、それぞれが今後10年以内に現実となる可能性について、あなたの予測を次の確率のなかから選んでほしい(可能性の低いものが多いので、確率の低いほうを細かく刻んである)。0・01パーセント未満、0・1パーセント、0・5パーセント、1パーセント、2パーセント、5パーセント、10パーセント、25パーセント、50パーセント以上。
- サウジアラビアが核兵器を開発する。
- ベネズエラのニコラス・マドゥロが大統領を辞任する。
- ロシアに女性大統領が誕生する。
- 新型コロナウイルスよりも感染力の強いウイルスによって、世界は新たなパンデミックに襲われる。
- ロシアのウラジーミル・プーチンは、憲法上次期大統領選に出馬できないため、プーチン夫人が代わりに出馬し、夫が脇から国を動かせるようにする。
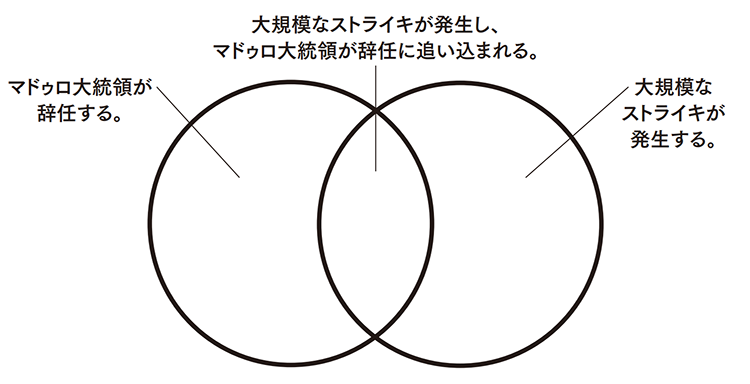
- ベネズエラで大規模なストライキと暴動が発生し、ニコラス・マドゥロ大統領が辞任に追い込まれる。
- 中国で、新型コロナウイルスよりも感染力の強い呼吸器系ウイルスがコウモリからヒトに感染し、新たなパンデミックが始まる。
- イランが核兵器を開発して地下核実験を断行し、これに対抗してサウジアラビアも核兵器を開発する。
わたしはある調査で、こうした問いを数百人に投げかけて答えてもらった。平均すると、回答者たちはロシアに女性大統領が誕生する可能性よりも、プーチン夫人が大統領になる可能性のほうが高いと考えた。またマドゥロ大統領が辞任する可能性よりも、ストライキと暴動で辞任に追い込まれる可能性のほうが高いと考えた。サウジアラビアが核兵器を開発する可能性よりも、イランの核実験に対抗して核兵器を開発する可能性のほうが高いと考えた。そして新たなパンデミックが発生する可能性よりも、中国のコウモリがパンデミックを引き起こす可能性のほうが高いと考えた。
これら4つの可能性の比較について、少なくとも1つくらいはあなたも同意するのではないだろうか? 実際、すべての問いに答えてくれた回答者の86パーセントがそうだった。
だがそれは確率の基本原則である「連言規則」──2つの事象の連言(AかつB)の確率は、どちらか一方(A、B)の確率より小さくなる──に反している〔連言とは2つ以上の文が「かつ」「そして」などでつながった命題のこと。合接、論理積ともいう〕。たとえば、カードの山のなかからスペードのカードを引き当てる確率は、偶数のスペードのカード(偶数かつスペード)を引き当てる確率よりも高い。スペードのなかには奇数のスペードもあるのだから。
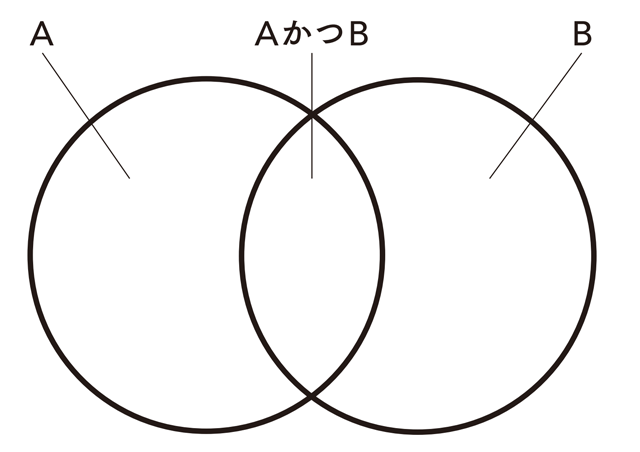
4つの可能性の比較に戻るが、いずれも第2のシナリオは2つの事象の連言で、その2つのうちの1つが第1のシナリオになっている。たとえば、「イランが核実験を行い、それに対抗してサウジアラビアが核兵器を開発する」は、「サウジアラビアが核兵器を開発する」場合の一部にすぎず、サウジアラビアが核兵器を開発するかもしれないシナリオはほかにもある(イスラエルに対抗する、ペルシャ湾地域の覇権を誇示するなど)。
したがって第2シナリオの可能性は第1シナリオより低くなる。同じ理屈により、「マドゥロが大統領を辞任する」可能性は、「一連のストライキと暴動がきっかけでマドゥロが大統領を辞任する」可能性より高くなければおかしい。
では多くの人の答えが逆になったのはなぜだろう? 何をどう考えると逆になるのだろうか? 実は、単文で表される事象は得てして包括的かつ抽象的になりがちで、脳の回路のどこにも引っかからずに流れていってしまう。一方、複文で表される事象はより鮮明なものになりうるし、なかでも物語風のものは、頭のなかで芝居を見るように想像することができる。直感確率は想像可能性に左右されるので、思い浮かべやすいものほど確からしく思えてしまう。そのせいでわたしたちは、エイモス・トヴェルスキーとダニエル・カーネマンが「連言錯誤」と呼ぶ罠に落ちる。連言で表された命題が成立する確率が、その連言を構成する個々の命題が成立する確率よりも、高いように思えてしまうという罠のことである。
これを逆手にとっているかに見えるのが評論家の予測で、往々にして生々しい語りに走り、確率などどこへやらといったものも見受けられる。ジャーナリストのロバート・カプランは、1994年に『アトランティック・マンスリー』の特集記事「アナーキーの到来(The Coming Anarchy)」で、次のような内容を予測した。21世紀の最初の数十年で、水などの希少資源をめぐって戦争が起こり、ナイジェリアがニジェール、ベナン、カメルーンを制圧し、アフリカをめぐって世界大戦が勃発し、アメリカ、カナダ、インド、中国、ナイジェリアが分裂し、アメリカのラテン系住民の多い地域はメキシコとの国境を取り払い、カナダのアルバータ州はアメリカのモンタナ州と合併し、アメリカの諸都市で犯罪が増加し、エイズがますます蔓延し、ほかにもさまざまな惨事、危機、崩壊が起こる。
しかしながら、この記事がセンセーションを巻き起こしているあいだにも(ビル・クリントン大統領もホワイトハウスでこの記事を回覧させた)、内戦の数、浄水へのアクセスをもたない人の割合、アメリカの犯罪率はどんどん下がっていった。3年を待たずにエイズの有効な治療法が実用化され、エイズによる死亡者数は減少しはじめた〔アメリカでは1995年がピークで、世界でも2000年代半ばには減少に転じた〕。そしてこの予測から四半世紀以上が経った今、国境はほとんど変わっていない。
連言錯誤を最初に説明したのはトヴェルスキーとカーネマンで、その際に彼らが取り上げた課題は「リンダ問題」として知られている。
◆リンダは31歳の独身で、はっきりものをいう頭のいい女性である。大学では哲学を専攻した。学生時代は差別や社会正義の問題に関心をもち、反核デモにも参加していた。
次の6つの項目のそれぞれについて、確率を予測せよ。
- リンダは小学校の教師をしている。
- リンダは女性解放運動に参加している。
- リンダは精神科ソーシャルワーカーをしている。
- リンダは銀行の窓口係をしている。
- リンダは保険外交員をしている。
- リンダは銀行の窓口係で、女性解放運動に参加している。
回答者は、リンダが銀行員である可能性よりも、フェミニストの銀行員である可能性のほうが高いと考えた。ここでもやはり人々は「A」の確率よりも「AかつB」の確率のほうが高いと判断したわけだ。この課題の人物設定は、往年の雰囲気を醸している。ベビーブーム時代に多かった「リンダ」という名前や、褒め言葉のようであってそうでない「頭のいい」という形容、時代遅れの抗議活動、失われつつある職業など、いかにも1980年代前半を思わせる。
しかし心理学の講師なら誰もが知るように、設定を変えても結果は変わらない。今日の聡明なアマンダについても、回答者の多くはアマンダが看護師である可能性より、アマンダがBLM(ブラック・ライヴズ・マター)運動に参加する看護師である可能性のほうが高いと考える。
リンダ問題はかなり強力に直感を支配している。「立ち読み①」で紹介したウェイソン選択課題の場合は、わたしたちは課題が抽象的だと間違うが、実生活に即した内容だとうまく調整できた。ところがリンダ問題では、「〈AかつB〉の確率は〈A〉の確率より小さいか等しい」という抽象的な法則には誰もが同意するのに、具体的な事例になったとたんにその逆だと思ってしまう。
この点について、生物学者で科学作家としても有名なスティーヴン・ジェイ・グールドは、わたしたちの多くを代弁してこう書いている。「連言命題は可能性が低いとわかっているのに、頭のなかでホムンクルス〔脳のなかにいるとされる小人〕がずっと飛び跳ねていて、わたしに向かって『でも彼女がただの銀行員だなんてことあるわけないだろ。説明をよく読めよ』と叫ぶのだ」
このホムンクルスは、相手を丸め込んで納得させるのに利用されることがある。たとえば検察官が、浜辺に打ち上げられた女性の死体以外に手がかりがないにもかかわらず、夫が彼女を絞め殺し、遺体を海に投げ込んだ可能性も否定できず、それは愛人と再婚するためであり、保険金で事業を始めるためだったなどと延々と主張したらどうだろうか。弁護人のほうもこれに対抗して、深夜にひったくりに襲われた可能性も排除できず、それが思いがけずひどい結果になったのではないかと弁論を繰り広げたらどうだろうか。
確率の法則からすれば、憶測を追加すればするほどシナリオが真である可能性は低くなるが、弁論においては逆に、説明を追加すればするほどシナリオの説得力が増していく。
ただ、多くの研究が明らかにしてきたのは、課題が「一度きりしか起こらない事象の確率」という不可解なものではなく、「相対的な頻度としての確率」を考えさせるものになっていれば、人は連言規則に従いやすくなるという点である。
たとえばリンダのような女性が1000人いるとしよう。そのうちの何人が銀行員だろうか? そのうちの何人が女性解放運動に参加している銀行員だろうか? こう問われると、わたしたちの“頭のなかのホムンクルス”は静かになり、“首尾一貫した人間”が外に出てこようとするので、連言錯誤に陥る人はだいぶ減る。
とはいえ、問いが頻度の形で提示され、回答者が頭のなかで銀行員のリンダを数えることによって連言錯誤を回避できるようになっていても、そうでない場合より少ないとはいえ、やはり連言錯誤に陥る人がいる。そしてその人数は、各選択肢を比較できるよう順番に示すのではなく、各選択肢を切り離して考えさせると過半数を占めるようになる(前者のほうが、下位集合の数が上位集合の数より多くなるという不条理に気づきやすい)。




